The Cost of Producing Electricity
Turbosteam
Calculation of Steam Cycle Energy Balance Using a Backpressure Steam Turbine
The cost per kWhr, the “cost of producing electricity”, is the cost of the energy which is taken out of the steam by the turbine generator system and converted into electricity. The following paper discusses calculation methods for determining this cost — a critical step in the process of evaluating cogeneration feasibility.
Using a backpressure (or pressure reducing) turbine in a cogeneration application is the most efficient form of producing electricity ever invented. This efficiency derives from the fact that the process steam is “used twice”; first to generate power, and second to satisfy process loads. Fuel-to-electric efficiencies typically range from 75 – 90%, whereas U.S. electric grid achieves just 33%. This efficiency difference leads to substantial savings for cogenerators, who can be producing electricity at 1.5 to 2.0 cents per kWhr, compared to utility rates of 4 to 10 cents per kWhr. It also means that a backpressure cogenerator can produce electricity with 1/3 of the fuel required by the grid — which means lower emissions of every pollutant including CO2.
Calculating the Cost of Producing Electricity – Simple Method:1
The simplest method of calculating the cost of producing electricity with a backpressure turbine is as follows:
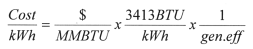
All that must be known is the cost of steam (or cost of fuel divided by boiler efficiency) in $/Million BTU steam, and generator efficiency, typically 95%. If a speed-reduction gear is required, its losses will be about 1.5%, but for this example, we will assume that a gear is not required. Assuming a generator efficiency of 95%, just divide your steam cost by 278:
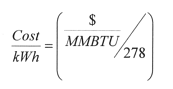
This will yield a figure that is accurate regardless of turbine type or turbine efficiency. This method and the more complex method described below both yield the same results via different routes.
Keep in mind that the above equation is true regardless of the specific turbine being used so long as there is a need for the heat present in the turbine exhaust. Every kWh produced with a particular facility’s turbine will cost the same, and that cost is dependent only upon the facility’s steam cost. The cost of power does not depend on turbine efficiency, but the amount of power does. A less efficient turbine will take fewer BTU’s from the steam, and make fewer kWh; a more efficient turbine will take more BTU’s from the steam and make more kWh. The total savings over a given period is the element that will differ.
Actual turbine efficiency or steam rate (also known as water rate) can be obtained from Turbosteam, or by using a steam flowmeter and kW meter for an existing installation.
Calculating the Cost of Producing Electricity – Energy Balance Method:
The following discussion covers the calculation of an energy balance across a process steam cycle. The steam cycle includes a boiler, pressure reducing station, and process equipment. We will consider the impact of a steam turbine generator installation designed to replace an existing pressure reduction valve. In this example, we will assume that a turbine selection has been made at a certain flow and at certain inlet and outlet conditions, and power output and steam rate have been determined. However, one can apply this same math to any specific installation.
1. Energy Balance Across the Turbine Generator System
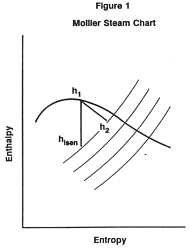
In reducing steam pressure, the turbine will extract some of the energy from the steam and convert it into torque (the generator subsequently converts this torque into electrical energy). In order to calculate how much energy the turbine extracts, it is necessary to find the enthalpy of the turbine exhaust steam. First establish inlet enthalpy h1 (see Figure 1) by using the inlet steam temperature and pressure to find the enthalpy either in the steam tables or on the Mollier chart.
In the case being examined, the proposed steam turbine generator system will operate between 280 psig, (dry and saturated steam), and 35 psig exhaust pressure. Process steam flow is 26,000 PPH (pounds of steam per hour). In a steam table reference, we find that the turbine inlet steam at 280 psig, dry and saturated, has enthalpy of:
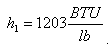
Then find hi s e n, the isentropic exhaust enthalpy (see Figure 1). Since in an isentropic process, inlet entropy is the same as exhaust entropy, the latter can be found by starting from h1 on the Mollier chart, and going vertically down the chart to the exhaust pressure. Read across to hi s e n, which in this case is 1066 BTU/lb.
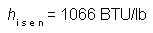
However, real turbines never achieve the theoretical limit imposed by hi s e n. The actual enthalpy removed by the turbine (h1-h2 in figure 1), divided by the theoretical maximum (h1– hi s e n) is referred to as the mechanical, or isentropic efficiency of the turbine. This efficiency is specific to a particular turbine under a particular set of conditions. In the conditions specified in this example, the turbine efficiency is 51%. Thus we can determine h2 as:
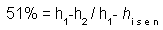
Substituting our known values and rearranging to solve for h2:
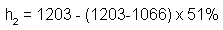
or:
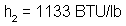
Since we know the exhaust pressure to be 35 psig, we can now refer back to our steam tables to determine that the exhaust steam will be of the following condition:
| Specific Enthalpy (h2 ) | 1133 BTU/lb |
| Pressure (P2 ) | 35 psig |
| Temperature (T2 ) | 281oF |
| Quality | 96% (4% moisture) |
Furthermore, we can now calculate the power production from the turbine generator – which is equivalent to the enthalpy removed from the steam, less friction and resistance losses in the generator:
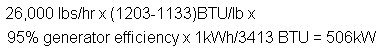
2. In the next section, we will consider how this impacts your process.
3. Energy Balance Across the Process Steam Cycle
Heat required by your process (Qprocess) is calculated based on the known condition (temperature and pressure) of the condensate which is returned to your boiler.2 Here 180 BTU/lb is assumed to be the enthalpy remaining in the condensate after your process heating loads have been satisfied (h3). Then:
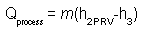
where m is pounds per hour of steam. Solving first for Qprocess:
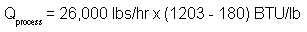
or:
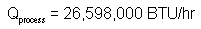
After the turbine-generator installation, the process will still require the same amount of heat flux. However, as we have already shown, the enthalpy h2 at the turbine exhaust is lower than the enthalpy that would have otherwise been retained in a PRV (h1).
Since we still need to provide Qprocess heat, we therefore must slightly increase our steam production to mnew, such that:
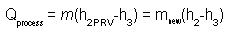
Solving for mnew:
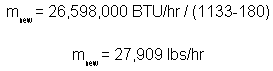
Thus, we must slightly increase our steam production (in this case, by 7.3%) to satisfy process thermal needs.3 However, we will also slightly increase the power output of the turbine due to rising mass flows — in this case, to 544 kW.
The cost of producing electricity is thus the cost of producing this additional 1,909 lbs/hr (a function solely of boiler efficiencies) divided by the turbine-generator electricity production (544 kW).
These calculations are shown schematically in the following two figures.
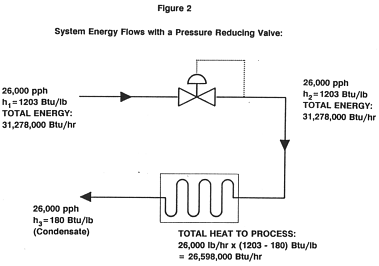
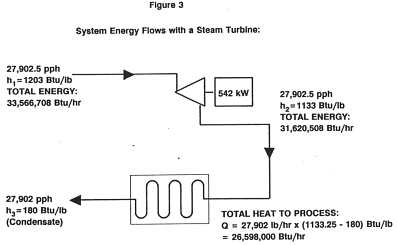
We now know that the turbine generator will generate 544 kW of electricity, and that to do so, we will require an increased steam flow of 1,909 lbs/hr to the process. The cost of electricity is thus the cost of this additional steam, divided by the power of output. Assuming a steam cost of $4 per thousand pounds:
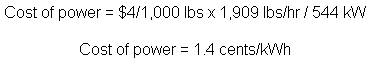
At average U.S. electricity rates of 6.6 cents/kWh, this system will thus save 5.2 cents per kWh, or:
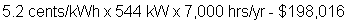
over a 7,000 hour operating year.
1Throughout this paper, we have used the most conservative possible estimates of turbine-generator efficiency. Most installations achieve even higher efficiencies, because the simplifying assumptions used in this generic set of thermodynamic calculations often differ from the practical considerations present in an operating steam plant. For a discussion of how these operating considerations may impact the economics of a particular facility, see part II of this paper: “Approaching Free Electricity: How the real world differs from thermodynamic models”.
2Note that this math assumes that 100% of your condensate is returned to your boiler. In real steam plants, actual condensate return is often less than 100% — and in many cases, this can serve to increase the effective power generation efficiency of a backpressure turbine generator. For details on how this might apply to a particular installation, see part II of this paper: “Approaching Free Electricity: How the real world differs from thermodynamic models”.
3Note that we are implicitly (and conservatively) assuming that the condensate return condition is fixed due to process temperature requirements. In many cases, processes will actually tolerate lower condensate temperatures, in which case the BTUs removed in the turbine generator would be replaced not by higher mass flows but rather by increased heat additions in the boiler, which is now heating colder condensate. The net economic impact is the same, but the actual operational impacts may differ.
Related Articles

Achieve Energy Savings in Plant Facilities

Eliminating Conveyor Concerns

OEE: Overall Equipment Effectiveness

What the Pump Was Designed to Do and Why it Doesn't Do it
What is Wrong with the Modern Centrifugal Pump?

The Full Circle of Engineering Education




